Introduction
Here we describe a two-stage demographic model with density dependence and interannual variability following Johnson et. al. (2020) with modifications noted in Hughes et al. (2025) and Dyson et al. (2022). Demographic rates vary with disturbance as estimated by Johnson et. al. (2020). A detailed description of the model is provided in Hughes et al. (2025) Section 2.4.
demographicCoefficients() selects the regression
coefficient values and standard errors for the desired model version
(see popGrowthTableJohnsonECCC for options) and then
samples coefficients from these Gaussian distributions for each
replicate population.
Next demographicRates() is used to apply the sampled
coefficients to the disturbance covariates to calculate expected
recruitment and survival according to the beta regression models
estimated by Johnson et al. (2020). Each population is optionally
assigned to quantiles of the Beta error distributions for survival and
recruitment. Using quantiles means that the population will stay in
these quantiles as disturbance changes over time, so there is persistent
variation in recruitment and survival among example populations.
Finally, we can use the estimated demographic rates to project population dynamics using a simple model with two age classes. Interannual variation in survival and recruitment is modelled using truncated beta distributions.
Simple demographic projection for a single example landscape
A simple case for demographic projection is multiple stochastic
projections from a single landscape that does not change over time.
First we define a disturbance scenario with 40% anthropogenic
disturbance and 2% fire disturbance. If we had spatial data for the
disturbance in our area of interest we could use
disturbanceMetrics() to directly calculate the disturbance.
(See Disturbance
Metrics vignette for an example).
disturbance <- data.frame(Anthro = 40, fire_excl_anthro = 2)We begin by sampling coefficients for 500 replicate populations using default Johnson et al. (2020) models “M1” and “M4”. The returned object is a list containing the coefficients and standard errors from the national model as well as the sampled coefficients and the quantiles that they have been assigned to.
popGrowthPars <- demographicCoefficients(500)
head(popGrowthPars$coefSamples_Survival$coefSamples)
#> Intercept Anthro Precision
#> [1,] -0.1530718 -0.0008907556 60.65168
#> [2,] -0.1399809 -0.0007155384 61.65165
#> [3,] -0.1612743 -0.0007628660 68.57570
#> [4,] -0.1420441 -0.0007747503 52.81483
#> [5,] -0.1370847 -0.0009535161 52.68192
#> [6,] -0.1329182 -0.0008050787 60.32032
head(popGrowthPars$coefSamples_Survival$coefValues)
#> Intercept Anthro Precision
#> <num> <num> <num>
#> 1: -0.142 -8e-04 63.43724
head(popGrowthPars$coefSamples_Survival$coefStdErrs)
#> Intercept Anthro Precision
#> <num> <num> <num>
#> 1: 0.007908163 0.000127551 8.272731
head(popGrowthPars$coefSamples_Survival$quantiles)
#> [1] 0.25345691 0.02880762 0.89123246 0.36007014 0.55806613 0.19063126Next we calculate sample demographic rates given sampled model
coefficients and disturbance metrics for our example landscape, setting
returnSample = TRUE so that the results returned contain a
row for each sample in each scenario. We set the initial population size
for each sample population to 100, and project population dynamics for
20 years using the caribouPopGrowth function with default
parameter values. Anthropogenic disturbance is high on this example
landscape, so the projected population growth rate for most sample
populations is below 1, but uncertainty in the model means that a few
sample populations persist.
rateSamples <- demographicRates(
covTable = disturbance,
popGrowthPars = popGrowthPars,
ignorePrecision = FALSE,
returnSample = TRUE,
useQuantiles = FALSE)
rateSamples$N0 <- 100
demography <- cbind(rateSamples,
caribouPopGrowth(N = rateSamples$N0,
numSteps = 20,
R_bar = rateSamples$R_bar,
S_bar = rateSamples$S_bar))
fds <- pivot_longer(demography, !(scnID:replicate) & !N0, names_to = "Metric",
values_to = "Amount")
d1 <- ggplot(fds, aes(x = as.factor(round(Anthro, 2)), y = Amount,
colour = fire_excl_anthro)) +
geom_violin(alpha = 0.4, color = "black") +
geom_point(shape = 21, size = 2, position = position_jitterdodge()) +
facet_wrap(~Metric, scales = "free") +
theme(legend.position = "none") +
xlab("Anthro")
plot(d1)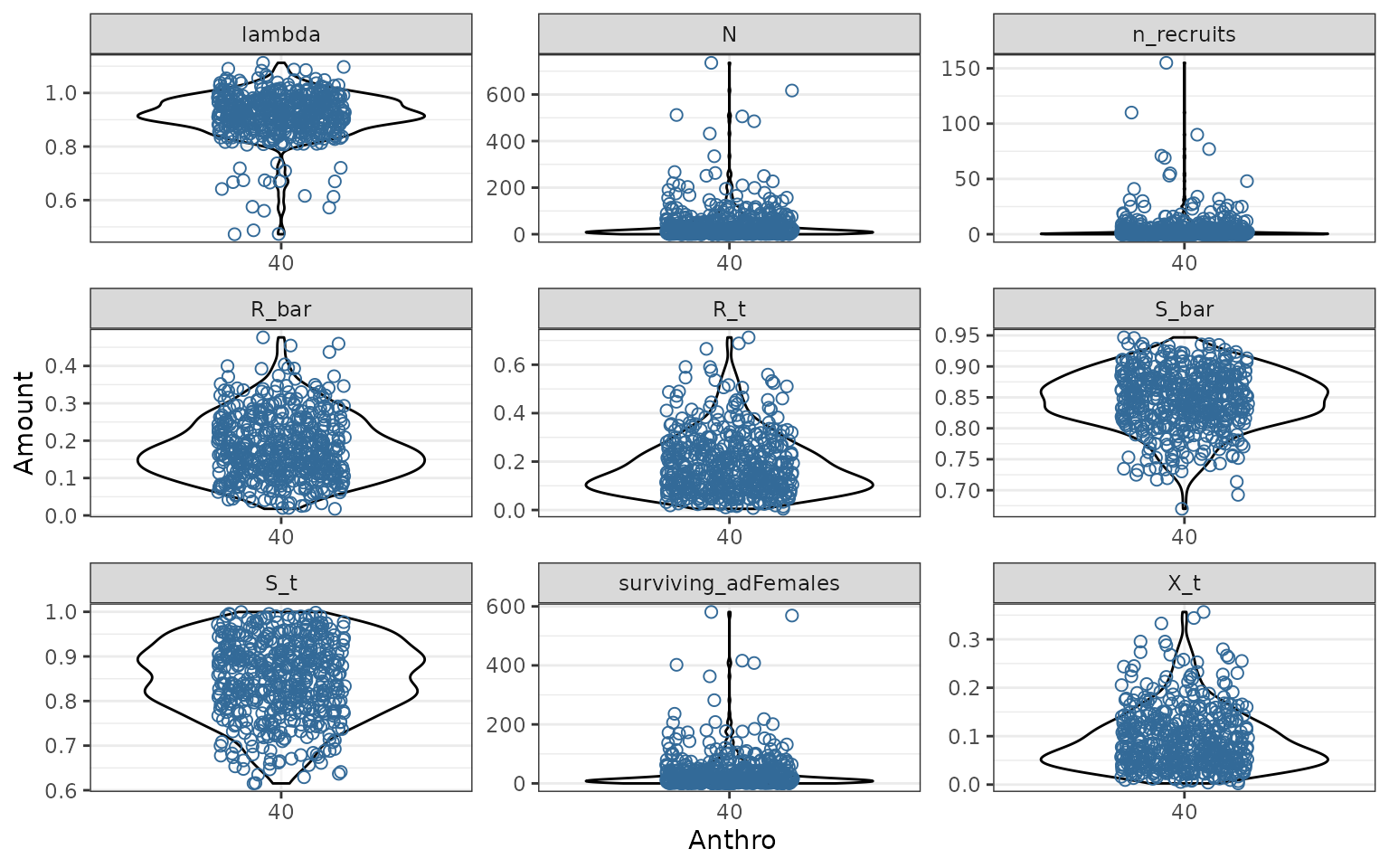
Effects of disturbance on demographic rates
We can project demographic rates over a range of landscape conditions to recreate figures 3 and 5 from Johnson et al. (2020) and see the effects of changing disturbance on model behaviour. First we create a table of disturbance scenarios across a range of different levels of fire and anthropogenic disturbance.
covTableSim <- expand.grid(Anthro = seq(0, 90, by = 2),
fire_excl_anthro = seq(0, 70, by = 10))
covTableSim$Total_dist = covTableSim$Anthro + covTableSim$fire_excl_anthroWe again sample coefficients from default models M1 and M4. The sample of 500 is used to calculate averages, while the sample of 35 is used to show variability among populations.
popGrowthPars <- demographicCoefficients(
500,
modelVersion = "Johnson",
survivalModelNumber = "M1",
recruitmentModelNumber = "M4",
populationGrowthTable = popGrowthTableJohnsonECCC
)
popGrowthParsSmall <- demographicCoefficients(
35,
modelVersion = "Johnson",
survivalModelNumber = "M1",
recruitmentModelNumber = "M4",
populationGrowthTable = popGrowthTableJohnsonECCC
)Next we calculate demographic rates given sampled model coefficients.
For the smaller sample we set returnSample = TRUE so that
the results returned contain a row for each sample in each scenario.
Setting useQuantiles = TRUE assigns each sample population
to a quantile of the regression model error distributions for survival
and recruitment, which allows us to see how demographic rates change.
For the larger sample we set returnSample = FALSE and the
result has one row for each scenario and includes summary statistics of
the uncertainty across the samples. We do this twice, once with
ignorePrecision = TRUE and once with
ignorePrecision = FALSE to demonstrate the effect of
considering the variance among populations around the National mean in
addition to the uncertainty about the coefficient estimates.
rateSamples <- demographicRates(
covTable = covTableSim,
popGrowthPars = popGrowthParsSmall,
ignorePrecision = FALSE,
returnSample = TRUE,
useQuantiles = TRUE
)
rateSummaries <- demographicRates(
covTable = covTableSim,
popGrowthPars = popGrowthPars,
ignorePrecision = FALSE,
returnSample = FALSE,
useQuantiles = FALSE
)
rateSummariesIgnorePrecision <- demographicRates(
covTable = covTableSim,
popGrowthPars = popGrowthPars,
ignorePrecision = TRUE,
returnSample = FALSE,
useQuantiles = FALSE
)Parameter uncertainty
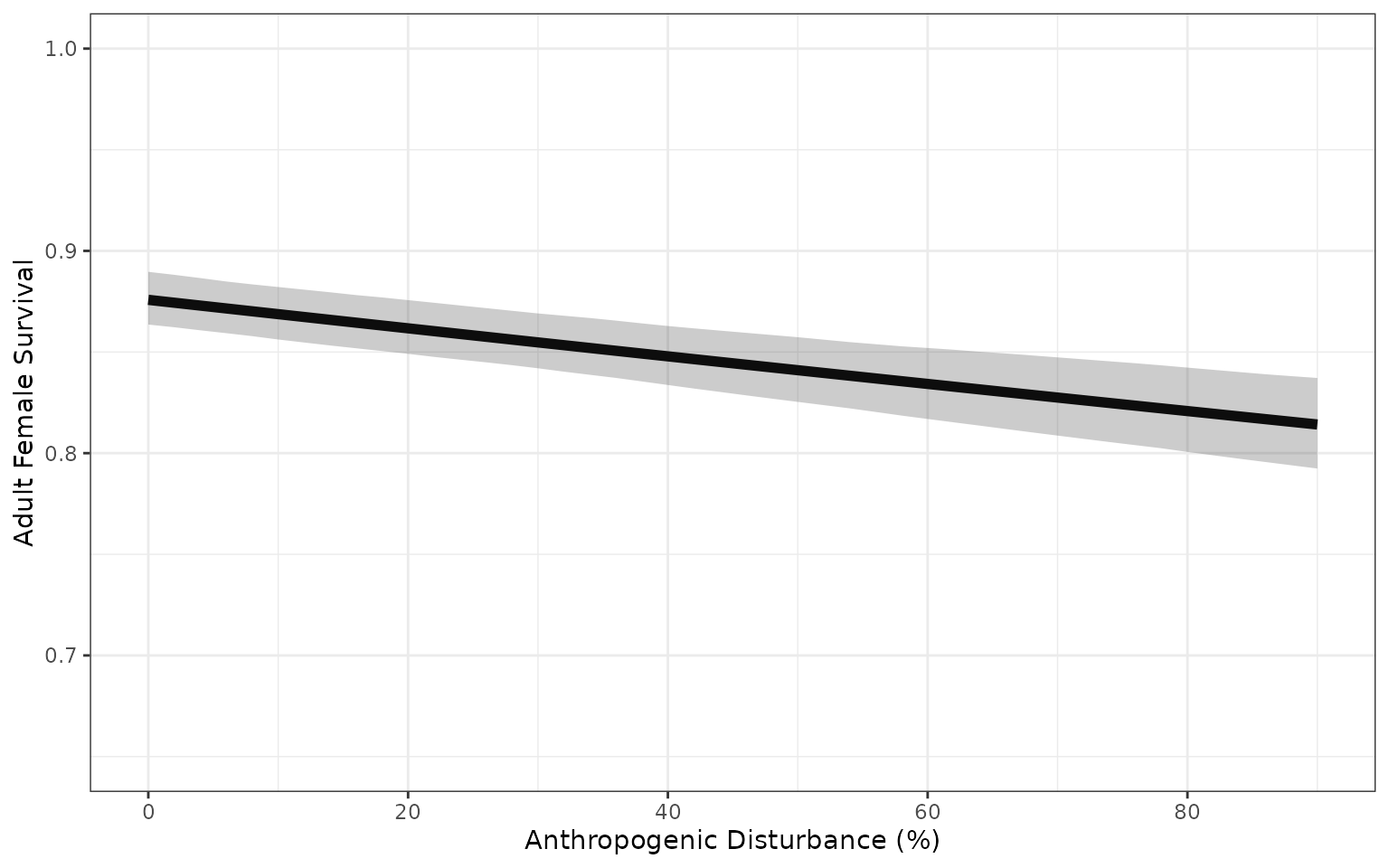
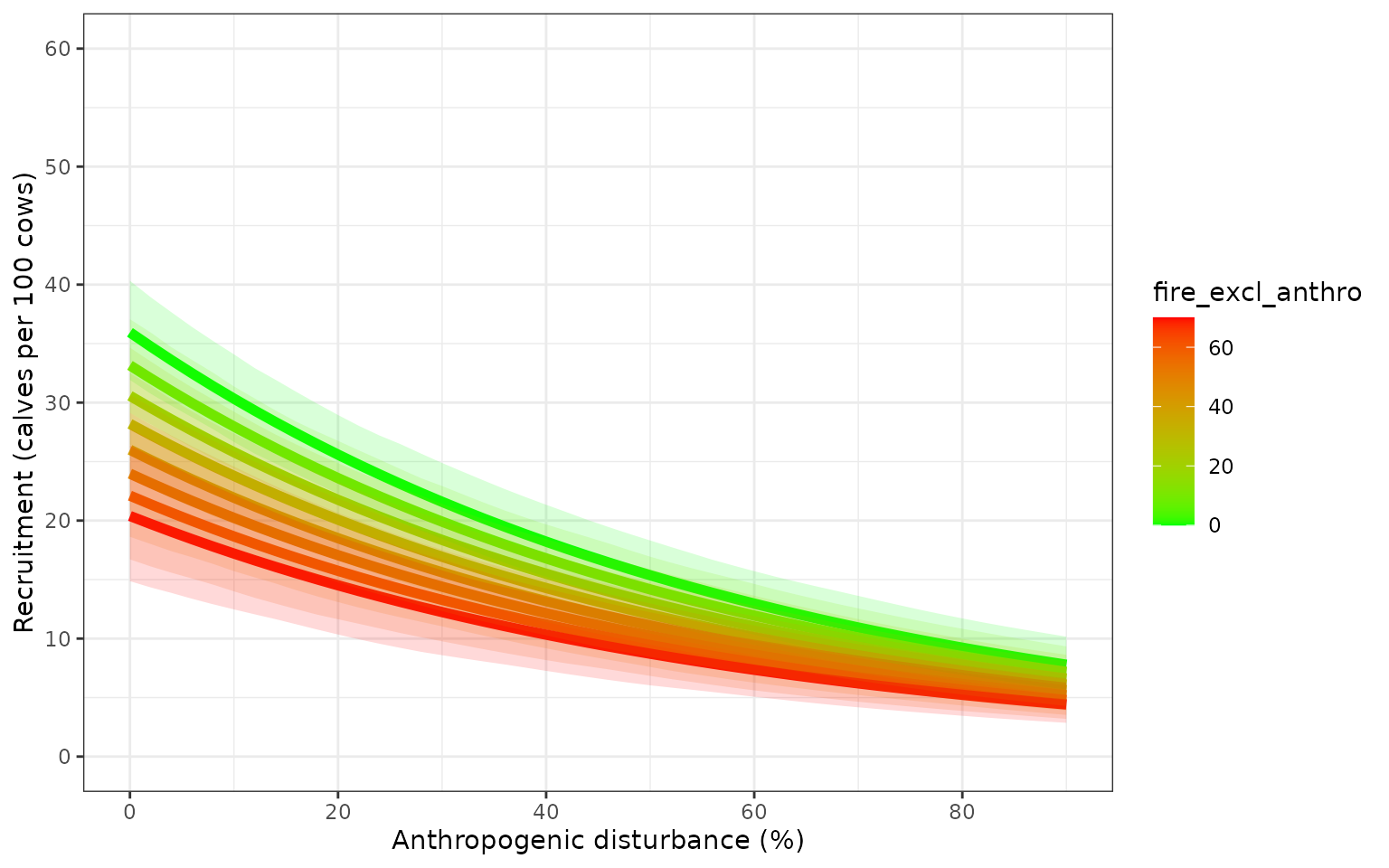
Variation in demographic rates from model that includes uncertainty
about the regression coefficients, and does not include additional
variation captured by the precision parameter of the Beta regression
model Ferrari and
Cribari-Neto 2004. The bands are the 2.5% and 97.5% quantiles of 500
sample parameter values.
Parameter uncertainty and precision
Variation in demographic rates from model that includes uncertainty about the regression coefficients and additional variation captured by the precision parameter of the Beta regression model Ferrari and Cribari-Neto 2004. Faint coloured lines show example trajectories of expected demographic rates in sample populations, assuming each sample population is randomly distributed among quantiles of the beta distribution, and each population remains in the same quantile of the beta distribution as disturbance changes.
#> Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
#> ℹ Please use `linewidth` instead.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.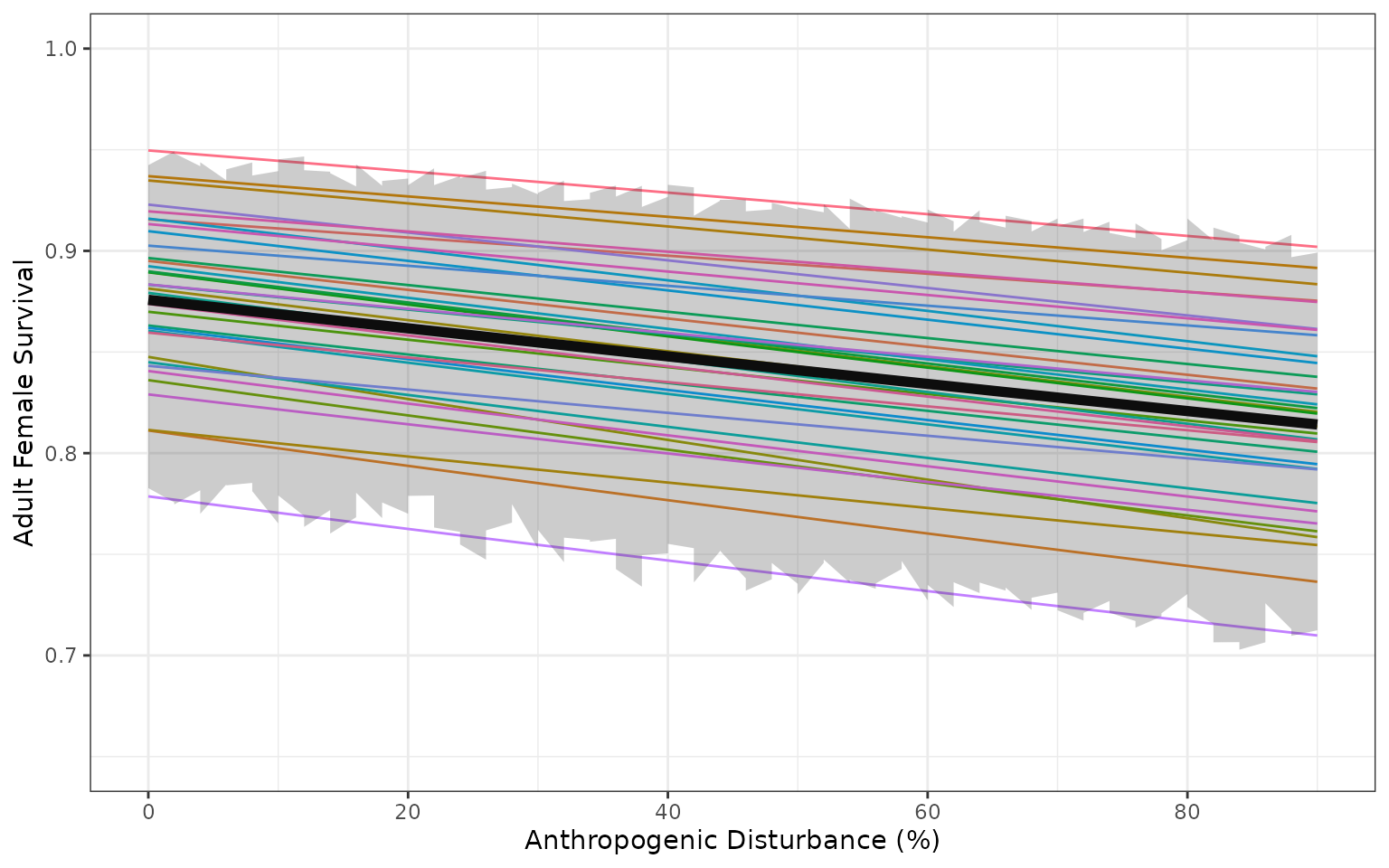
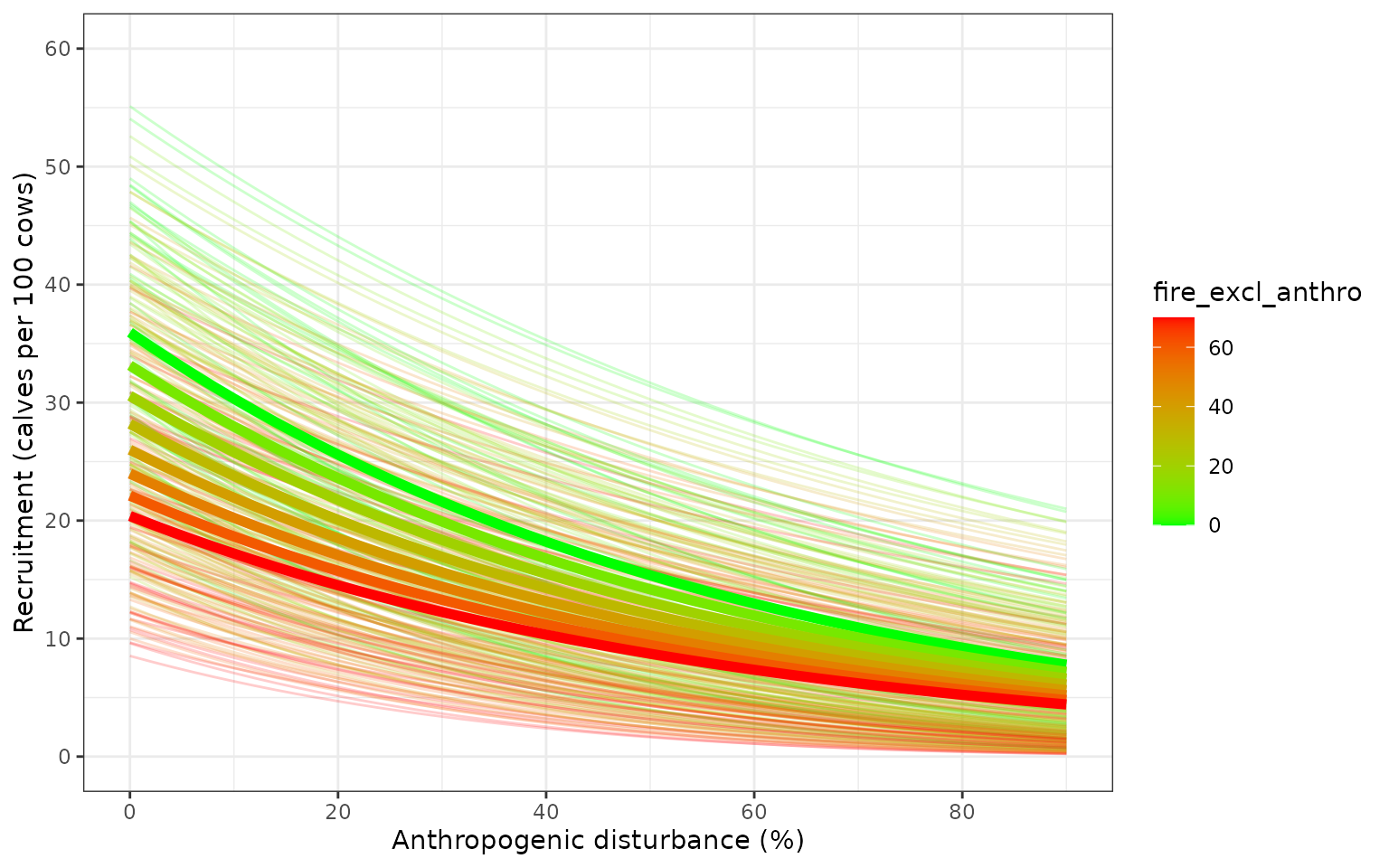
Projection of population growth over time on a changing landscape
In this example, we project 35 sample populations for 50 years on a
landscape where the anthropogenic disturbance footprint is increasing by
5% per decade. We set interannualVar = FALSE,
K = FALSE, and probOption = "continuous" to
use a simpler model without interannual variability, density dependence,
or discrete numbers of animals, as in Stewart et al. 2023.
numTimesteps <- 5
stepLength <- 10
N0 <- 100
AnthroChange <- 5 #For illustration assume 5% increase in anthropogenic disturbance footprint each decade
# at each time, sample demographic rates and project, save results
pars <- data.frame(N0 = N0)
for (t in 1:numTimesteps) {
covariates <- disturbance
covariates$Anthro <- covariates$Anthro + AnthroChange * (t - 1)
rateSamples <- demographicRates(
covTable = covariates,
popGrowthPars = popGrowthParsSmall,
ignorePrecision = FALSE,
returnSample = TRUE,
useQuantiles = TRUE
)
if (is.element("N", names(pars))) {
pars <- subset(pars, select = c(replicate, N))
names(pars)[names(pars) == "N"] <- "N0"
}
pars <- merge(pars, rateSamples)
pars <- cbind(pars,
caribouPopGrowth(pars$N0,
R_bar = pars$R_bar, S_bar = pars$S_bar,
numSteps = stepLength, interannualVar = FALSE,
K = FALSE, probOption = "continuous"))
# add results to output set
fds <- subset(pars, select = c(replicate, Anthro, S_bar, R_bar, N, lambda))
fds$replicate <- as.numeric(gsub("V", "", fds$replicate))
names(fds) <- c("Replicate", "anthro", "survival", "recruitment", "N", "lambda")
fds <- pivot_longer(fds, !Replicate, names_to = "MetricTypeID", values_to = "Amount")
fds$Timestep <- t * stepLength
if (t == 1) {
popMetrics <- fds
} else {
popMetrics <- rbind(popMetrics, fds)
}
}
popMetrics$MetricTypeID <- as.character(popMetrics$MetricTypeID)
popMetrics$Replicate <- paste0("x", popMetrics$Replicate)
popMetrics <- subset(popMetrics, !MetricTypeID == "N")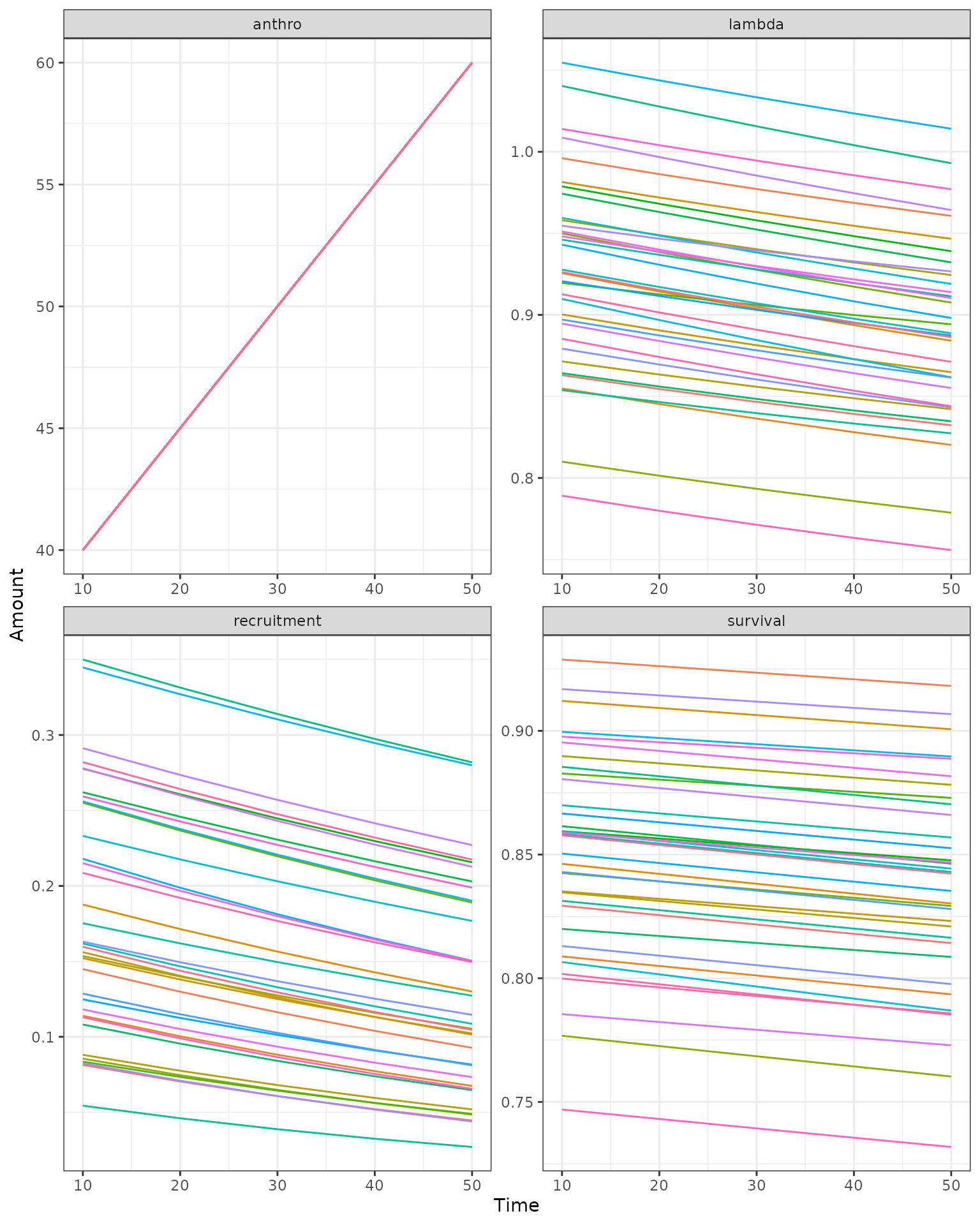
References
Dyson, M., Endicott, S., Simpkins, C., Turner, J. W., Avery-Gomm, S., Johnson, C. A., Leblond, M., Neilson, E. W., Rempel, R., Wiebe, P. A., Baltzer, J. L., Stewart, F. E. C., & Hughes, J. (2022). Existing caribou habitat and demographic models need improvement for Ring of Fire impact assessment: A roadmap for improving the usefulness, transparency, and availability of models for conservation. https://doi.org/10.1101/2022.06.01.494350
Ferrari S, Cribari-Neto F (2004) Beta Regression for Modelling Rates and Proportions. Journal of Applied Statistics 31:799–815. https://doi.org/10.1080/0266476042000214501
Hughes, J., Endicott, S., Calvert, A.M. and Johnson, C.A., 2025. Integration of national demographic-disturbance relationships and local data can improve caribou population viability projections and inform monitoring decisions. Ecological Informatics, 87, p.103095. https://doi.org/10.1016/j.ecoinf.2025.103095
Johnson, C.A., Sutherland, G.D., Neave, E., Leblond, M., Kirby, P., Superbie, C. and McLoughlin, P.D., 2020. Science to inform policy: linking population dynamics to habitat for a threatened species in Canada. Journal of Applied Ecology, 57(7), pp.1314-1327. https://doi.org/10.1111/1365-2664.13637
Novomestky F, Nadarajah S (2016) Package ‘truncdist.’ Version 1.0-2URL https://CRAN.R-project.org/package=truncdist
Stewart, F.E., Micheletti, T., Cumming, S.G., Barros, C., Chubaty,
A.M., Dookie, A.L., Duclos, I., Eddy, I., Haché, S., Hodson, J. and
Hughes, J., 2023. Climate‐informed forecasts reveal dramatic local
habitat shifts and population uncertainty for northern boreal caribou.
Ecological Applications 33:e2816.
https://doi.org/10.1002/eap.2816